LeNet：初试卷积神经网络

你可以认为LeNet是第一个卷积神经网络成功的应该用。LeNet的原论文是Gradient-Based Learning Applied to Document Recognition。

在“多层感知机”一节里我们构造了一个含单隐藏层的多层感知机模型来对Fashion-MNIST数据集中的图像进行分类。每张图像高和宽均是28像素。我们将图像中的像素逐行展开，得到长度为784的向量，并输入进全连接层中。然而，这种分类方法有一定的局限性。

1. 图像在同一列邻近的像素在这个向量中可能相距较远。它们构成的模式可能难以被模型识别。
2. 对于大尺寸的输入图像，使用全连接层容易导致模型过大。假设输入是高和宽均为1,0001,000像素的彩色照片（含3个通道）。即使全连接层输出个数仍是256，该层权重参数的形状也是3,000,000×2563,000,000×256：它占用了大约3 GB的内存或显存。这会带来过于复杂的模型和过高的存储开销。

卷积层尝试解决这两个问题。一方面，卷积层保留输入形状，使图像的像素在高和宽两个方向上的相关性均可能被有效识别；另一方面，卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算，从而避免参数尺寸过大。

LeNet的名字来源于LeNet论文的第一作者Yann LeCun。LeNet展示了通过梯度下降训练卷积神经网络可以达到手写数字识别在当时最先进的结果。这个奠基性的工作第一次将卷积神经网络推上舞台，为世人所知。

LeNet 模型

LeNet缠身过很多不同的变种。在这我们讨论LeNet-5。

LeNet-5是一个专门为手写数字识别而设计的经典卷积神经网络。在MNIST数据集上，LeNet-5能够达到大约99.4%的准确率。基于LeNet-5设计的手写数字识别系在20世纪90年代被广泛应用于美国的许多家银行进行支票的手写数字识别。

根据LeNet-5作者Yann LeCun教授公开发表的论文内容，可知LeNet-5公有8层（包括输入和输出层），之所以它被称为LeNet-5是因为其卷积部分（包含卷积和下采样）层数的总数是5。

与近几年的卷积神经网络相比较，LeNet-5的网络规模比较小，但是包含了构成现代卷积神经网络的基本组件——卷积层、池化层、全连接层。再复杂的卷积神经网络也会包含这些基本的组件。所以某种意义上我们将LeNet视为卷积神经网络的“开山之作”。

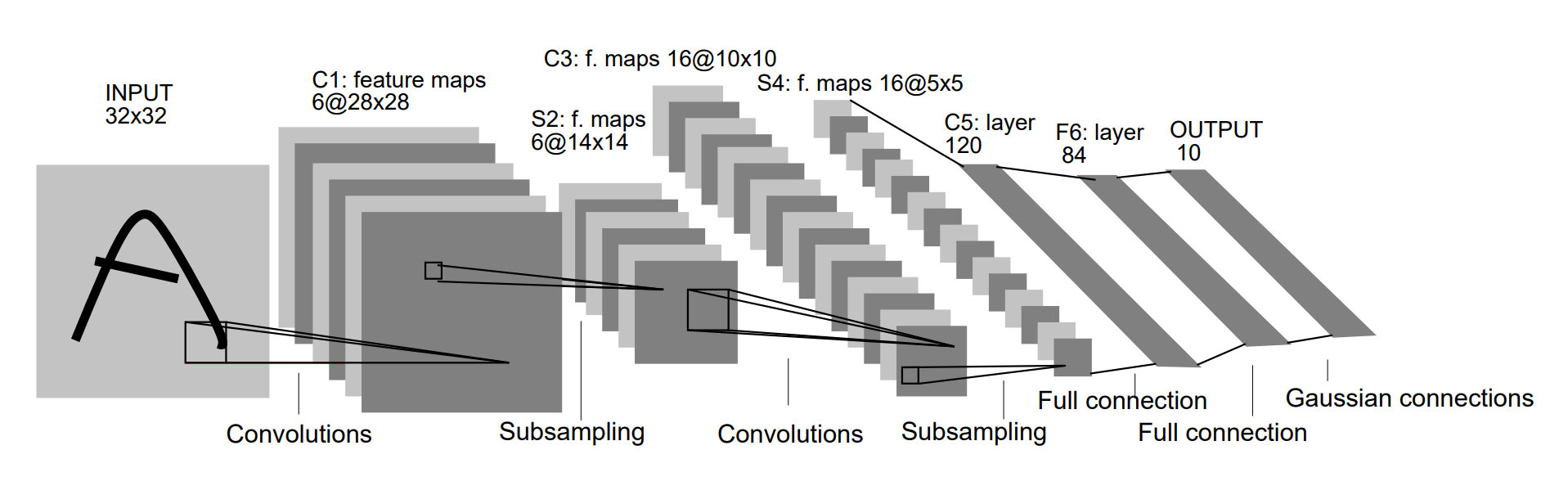
上图是在LeNet-5相应论文中找到的网络结构图，在上图中，C代表卷积层，卷积操作的目的是使信号特征增强并降低噪音。用S代表下采样层，执行的是池化操作，利用图像局部相关性原理，对图像进行子抽样，这样可以减少数据量，同时也保留一定的有用的信息。

现在我们讨论LeNet-5的模型结构。LeNet-5共有8层，其中包含了1个输入层、3个卷积层、2个下采样层，2个全连接层。它的网络结构可以被描述为：

LeNet-5：输入-（1.卷积-2.下采样-3.卷积-4.下采样-5.卷积）-全连接-全连接

1. 第一层：输入层，输入的是32x32分辨率的灰度图。注意，MNIST数据集中图片的大小是28x28。这样做的原因是希望最高层特征检测感受野的中心能够收集更多潜在的明显特征（如转折、断点等）。
2. 第二层：C1层是一个卷积层，由6个特征图组成。这个卷积层的核尺寸是5x5，深度是6。
3. 第三层：S2是一个下采样层，通过2x2的下采样，得到了深度为6（和上一层一样）的14x14特征图。也就是说，S2中的每一个特征图的每一个单元都与C1层输出的特征图中的2x2大小的位置相连。
4. 第四层：C3是一个卷积层，由第三层的图像通过一个深度为16，大小为5x5的卷积核卷积得到。注意，本层输出的每个特征图并不是一对一地与上一层的6个特征图相连，它们相连的关系是：
5. 第五层：S4是一个下采样层，有16个5x5大小的特征图，每一个都与C3层输出的特征图中的2x2大小的位置相连。
6. 第六层：C5是一个卷积层，其中有120个大小为5x5的卷积核对上一层的输出进行卷积。尽管这层在论文中是一个卷积层，但是基本与全连接层没有区别，在代码中常将其直接写为全连接层。
7. 第七层：F6是一个全连接层，有84个神经元，与上一层C5构成全连接关系。
8. 第八层：输出层也是一个全连接层，共有十个神经元，分别代表数字0~9。

使用代码实现

导入数据集

首先我们导入手写数字识别的数据集，并且给一些初始化的流程。

import tensorflow as tf
from tensorflow.keras import datasets, layers, initializers

(training_x, training_y), (testing_x, testing_y) = datasets.mnist.load_data()
training_x = (training_x.astype('float32') / 255.)
testing_x = (testing_x.astype('float32') / 255.)
training_x = tf.reshape(training_x, (training_x.shape[0], training_x.shape[1], training_x.shape[2], 1))
testing_x = tf.reshape(testing_x, (testing_x.shape[0], testing_x.shape[1], testing_x.shape[2], 1))
batch_size = 100

training_dataset = tf.data.Dataset.from_tensor_slices((training_x, training_y))
training_dataset = training_dataset.batch(batch_size)
testing_dataset = tf.data.Dataset.from_tensor_slices((testing_x, testing_y))
testing_dataset = testing_dataset.batch(batch_size)

上面这段你应该会对它越来越熟悉，因为它将被经常使用。整个过程的详细解释请参考常见代码块中有关数据集的部分。

定义模型

接下来我们定义LeNet5的往网络模型。在tensorflow的模型中我们往往不定义输入层，所以除去输入层Lenet5的模型应该有七层：

model = tf.keras.models.Sequential([
    # 1.第一个卷积层
    tf.keras.layers.Conv2D(filters=32,kernel_size=5,activation='sigmoid',input_shape=(28,28,1)),
    # 2.最大池化
    tf.keras.layers.MaxPool2D(pool_size=2, strides=2),
    # 3.第二个卷积层
    tf.keras.layers.Conv2D(filters=64,kernel_size=5,activation='sigmoid'),
    # 4.最大池化
    tf.keras.layers.MaxPool2D(pool_size=2, strides=2),
    # 5.打平以便进入全连接
    tf.keras.layers.Flatten(),
    # 6.第一个全连接层
    tf.keras.layers.Dense(512,activation='sigmoid'),
    # 7.第一个全连接层
    tf.keras.layers.Dense(10,activation='sigmoid')
])

还有一种等效的写法看上去“更专业”：

class LeNetModel(tf.keras.Model):
    def __init__(self):
        super(LeNetModel, self).__init__()
        # 1.第一个卷积层
        self.conv1 = layers.Conv2D(filters=32, kernel_size=(5, 5), padding='SAME', activation=tf.nn.sigmoid, use_bias=True, bias_initializer=initializers.Zeros)
        # 2.最大池化
        self.maxpool1 = layers.MaxPool2D(pool_size=(2, 2), strides=(2, 2), padding='SAME')
        # 3.第二个卷积层
        self.conv2 = layers.Conv2D(filters=64, kernel_size=(5, 5), padding='SAME', activation=tf.nn.sigmoid, use_bias=True, bias_initializer=initializers.Zeros)
        # 4.最大池化
        self.maxpool2 = self.maxpool1 = layers.MaxPool2D(pool_size=(2, 2), strides=(2, 2), padding='SAME')
        # 5.打平以便进入全连接
        self.flatten = layers.Flatten()
        # 6.第一个全连接层
        self.fc1 = layers.Dense(units=512, activation=tf.nn.sigmoid, use_bias=True, bias_initializer=initializers.Zeros)
        # 7.第一个全连接层
        self.fc2 = layers.Dense(units=10, activation=tf.nn.sigmoid, use_bias=True, bias_initializer=initializers.Zeros)

    # 定义前向传播的方法
    def call(self, inputs, training=None, mask=None):
        result = self.conv1(inputs)
        result = self.maxpool1(result)
        result = self.conv2(result)
        result = self.maxpool2(result)
        result = self.flatten(result)
        result = self.fc1(result)
        result = self.fc2(result)
        return result
# 创建一个模型实例
model = LeNetModel()

这两段代码具有相同效果。你只需要选择其中一段。不难看出，这两段代码的主要区别就是低一段中Keras API的使用率更高，它使用了Sequential，省去了很多代码量。在研究过程中，我更推荐你提高Keras API的使用率，这样会让你的代码简洁、易读、维护性强。你可以在之后的一篇叫做新玩具：Keras API的文章中大致了解Keras。

定义损失函数和优化器

# 损失函数
loss_fun = tf.losses.SparseCategoricalCrossentropy(name='loss_fun')
# 表示训练和测试损失
train_loss = tf.metrics.Mean(name='train_loss')
test_loss = tf.metrics.Mean(name='train_loss')
# 表示训练和测试准确性
train_acc = tf.metrics.SparseCategoricalAccuracy(name='train_acc')
test_acc = tf.metrics.SparseCategoricalAccuracy(name='train_acc')
# 使用Adam优化器
optimizer = tf.optimizers.Adam()

定义训练步骤

@tf.function
def training_step(images, labels):
    with tf.GradientTape() as tape:
        pred = model(images)
        loss = loss_fun(labels, pred)
        gradients = tape.gradient(loss, model.trainable_variables)
        optimizer.apply_gradients(zip(gradients, model.trainable_variables))
        train_loss(loss)
        train_acc(labels, pred)

定义测试步骤

@tf.function
def verify_on_test(images, labels):
    pred = model(images)
    loss = loss_fun(labels, pred)
    test_loss(loss)
    test_acc(labels, pred)

开始训练和测试

epochs = 40
for ep in range(epochs):
    for images, labels in training_dataset:
        training_step(images, labels)
    for images, labels in testing_dataset:
        verify_on_test(images, labels)
    template = 'Epoch{}, loss:{}, Acc:{}%, test_loss:{}, test_acc:{}%'
    print(template.format(ep + 1,
                          train_loss.result(),
                          train_acc.result() * 100.,
                          test_loss.result(),
                          test_acc.result() * 100.))

你可以使用Keras API在几行之内完成损失函数和优化器的声名、模型的训练和测试。这里把这几部分展开来写，是为了让读者了解整个过程。如果你想立即了解使用Keras API的写法，请参考LeNet代码实现。

输出的内容

如果没出意外的话，你会看到这样的输出：

Epoch1, loss:2.0541832447052, Acc:22.036666870117188%, test_loss:0.5713689923286438, test_acc:82.48999786376953%
Epoch2, loss:1.1895983219146729, Acc:56.12999725341797%, test_loss:0.39248934388160706, test_acc:87.92499542236328%
Epoch3, loss:0.8565776348114014, Acc:68.79499816894531%, test_loss:0.3101097643375397, test_acc:90.48999786376953%
Epoch4, loss:0.6785899996757507, Acc:75.492919921875%, test_loss:0.2617659866809845, test_acc:91.9749984741211%
Epoch5, loss:0.5668724179267883, Acc:79.6520004272461%, test_loss:0.2300516664981842, test_acc:92.94599914550781%
Epoch6, loss:0.48972204327583313, Acc:82.508056640625%, test_loss:0.20772139728069305, test_acc:93.63666534423828%
Epoch7, loss:0.432917982339859, Acc:84.59904479980469%, test_loss:0.19109736382961273, test_acc:94.1500015258789%
Epoch8, loss:0.3891405165195465, Acc:86.20708465576172%, test_loss:0.17826248705387115, test_acc:94.52625274658203%
Epoch9, loss:0.3542391359806061, Acc:87.48480987548828%, test_loss:0.1680169403553009, test_acc:94.83333587646484%
Epoch10, loss:0.32566919922828674, Acc:88.52400207519531%, test_loss:0.15959297120571136, test_acc:95.0770034790039%

可以看出，识别的准确率在不断提高。随着Epoch继续增加，准确率会达到99%以上。

尝试修改网络模型

为了方便展示和修改，我们将使用那段Sequential API的写法进行修改和展示：

# 这是原来的代码
model = tf.keras.models.Sequential([
    tf.keras.layers.Conv2D(filters=32,kernel_size=5,activation='sigmoid',input_shape=(28,28,1)),
    tf.keras.layers.MaxPool2D(pool_size=2, strides=2),
    tf.keras.layers.Conv2D(filters=64,kernel_size=5,activation='sigmoid'),
    tf.keras.layers.MaxPool2D(pool_size=2, strides=2),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(512,activation='sigmoid'),
    tf.keras.layers.Dense(10,activation='sigmoid')
])

自习想想，仅识别包含所有英文字母和数字在内的手写数字似乎并不需要提取太多阶段的特征，所以我们可以试着把卷积层的卷积核深度改小一点，然后再把全连接层的节点数目弄小一点：

model = tf.keras.models.Sequential([
    # 将第一个卷积层卷积核的深度从32改为6
    tf.keras.layers.Conv2D(filters=6,kernel_size=5,activation='sigmoid',input_shape=(28,28,1)),
    tf.keras.layers.MaxPool2D(pool_size=2, strides=2),
    # 将第二个卷积层卷积核的深度从64改为16
    tf.keras.layers.Conv2D(filters=16,kernel_size=5,activation='sigmoid'),
    tf.keras.layers.MaxPool2D(pool_size=2, strides=2),
    tf.keras.layers.Flatten(),
    # 将第一个卷积层卷积核的深度从512改为128
    tf.keras.layers.Dense(128,activation='sigmoid'),
    tf.keras.layers.Dense(10,activation='sigmoid')
])

替换到原来的代码中，训练时输出：

Epoch1, loss:1.0259242057800293, Acc:67.72000122070312%, test_loss:0.275608092546463, test_acc:92.37999725341797%
Epoch2, loss:0.6220030188560486, Acc:80.74666595458984%, test_loss:0.21593712270259857, test_acc:93.76499938964844%
Epoch3, loss:0.46325913071632385, Acc:85.74610900878906%, test_loss:0.18218189477920532, test_acc:94.63666534423828%
Epoch4, loss:0.37573355436325073, Acc:88.46541595458984%, test_loss:0.15966089069843292, test_acc:95.26499938964844%
Epoch5, loss:0.3193082809448242, Acc:90.21499633789062%, test_loss:0.14330348372459412, test_acc:95.7300033569336%
Epoch6, loss:0.27947044372558594, Acc:91.44611358642578%, test_loss:0.13075928390026093, test_acc:96.09000396728516%
Epoch7, loss:0.2496245801448822, Acc:92.36809539794922%, test_loss:0.1207747831940651, test_acc:96.37857055664062%
Epoch8, loss:0.22630730271339417, Acc:93.0893783569336%, test_loss:0.11260426789522171, test_acc:96.625%
Epoch9, loss:0.20751149952411652, Acc:93.67203521728516%, test_loss:0.10577848553657532, test_acc:96.83222198486328%
Epoch10, loss:0.191986545920372, Acc:94.149169921875%, test_loss:0.09998638927936554, test_acc:97.00499725341797%

可以看到，比起原来的网络结构，在第10个Epoch，新的网络结构的准确率达到97%左右，比原网络的95%左右要高；同时你也会发现，新的网络训练和运算起来比原网络快了不止一倍。

整个Pure代码

请参考LeNet代码实现